Understanding Statistical Tolerance Analysis
Definition of Statistical Tolerance Analysis
A statistical tolerance analysis is when you take the variation of a set of inputs to calculate the expected variation of an output of interest. In mechanical engineering, a product design is composed of multiple features, each with tolerance values that control the variable aspects of those features. Statistical tolerance analysis is used to understand how these tolerances contribute the various performance characteristics of the design.
1D Tolerance Stackup
The simplest form of tolerance analysis is the single direction, 1D Tolerance Stackup. A 1D Tolerance Stackup is created by creating a cross section of a model and adding the tolerance values for each feature in a straight line. The variation in each contributes to the overall output/outcome.
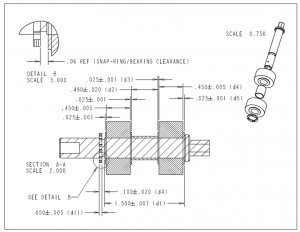
Worst-Case Analysis vs RSS (Root-Sum Squared) Statistical Analysis
In a Worst-Case Analysis, each dimension will have a minimum and maximum value that represents the range of acceptability for that dimension. Worst-Case answers the question, if I take the maximum range on each input, what is the maximum range for the measurement of interest or stackup? We are therefore dealing with the limits of acceptability and not probability.
RSS (Root-Sum Squared) Statistical Analysis does not focus on the extreme values, but focuses on the distribution of the variation for each dimension. Each dimension will have a unique distribution of values based on the manufacturing process. Tool wear, operator differences, changes in material and environment all contribute to variation in the dimension value. Each dimension has its own distribution curve.
When you combine the probabilities for each dimension (each separate curve) you get the probability for the total and therefore the distribution curve of the total. Statistical analysis answers the question, given the distribution of variation on each dimension what is the probability that my performance characteristic will fall within defined acceptable limits. The limitation of RSS is that it assumes all inputs are normally distributed and all performance characteristics have a linear relationship with the dimension. These assumptions do not account for the breadth of conditions that exist in typical scenarios found in manufacturing.
Second Order Tolerance Analysis
Because manufacturing methods vary for different types of parts, the distribution moments or parameters change as well. RSS only uses standard deviation and does not include the higher moments of skewness and kurtosis that better characterize the effects tool wear, form aging and other typical manufacturing scenarios. Second Order Tolerance Analysis incorporates all distribution moments: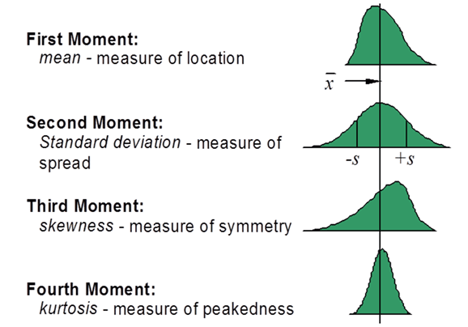
Second Order Tolerance Analysis is also needed to determine what your output is going to be when the assembly function is not linear. In typical mechanical engineering scenarios kinematic adjustments and other assembly behaviors result in non-linear assembly functions. Second order calculations are much more complex so hand calculations are not advisable but the computation accuracy is greatly improved and becomes viable within a tolerance analysis software package.
Summary of Statistical Tolerance Analysis for practical useage
The choice in tolerance analysis method is based on many factors, but the can be summarized as “Which method best matches the manufacturing and inspection process of the assembly”. For simple fit problems, a 1D stack-up may be sufficient. RSS is sufficient for the small number of scenarios where the inputs are normal and the assembly relationships are linear. For all other scenarios, Second Order Tolerance Analysis is required to address the real world of manufacturing.
How does Sigmetrix’ Software & Training solutions enable engineers & designers to calculate precise Statistical Tolerance Analysis?
Our systems are designed to integrate within the primary 3D cad environments in which manufacturers design parts and assemblies. Enabling them to utilize Geometric Dimensions & Tolerancing reporting to create efficient Tolerance Analysis and Variations for viable products. Thus creating an early modeling method prior to production and assembly for increased ROI creating the need for a world renowned GD&T software. For more information the relationship of quality and profitability in manufacturing click here, or read through our white papers and case studies throughout the website.

